Temporal Horizons in Forecasting: A Performance-Learnability Trade-off
Preprint available on arXiv. See the full paper here.
When training machine learning models to predict the future, a critical question emerges: how far ahead should we train them to forecast? This seemingly simple choice hides a fundamental trade-off that we've uncovered in our recent work. Too short a horizon might miss crucial long-term patterns, while too long a horizon can make the training process exponentially harder.
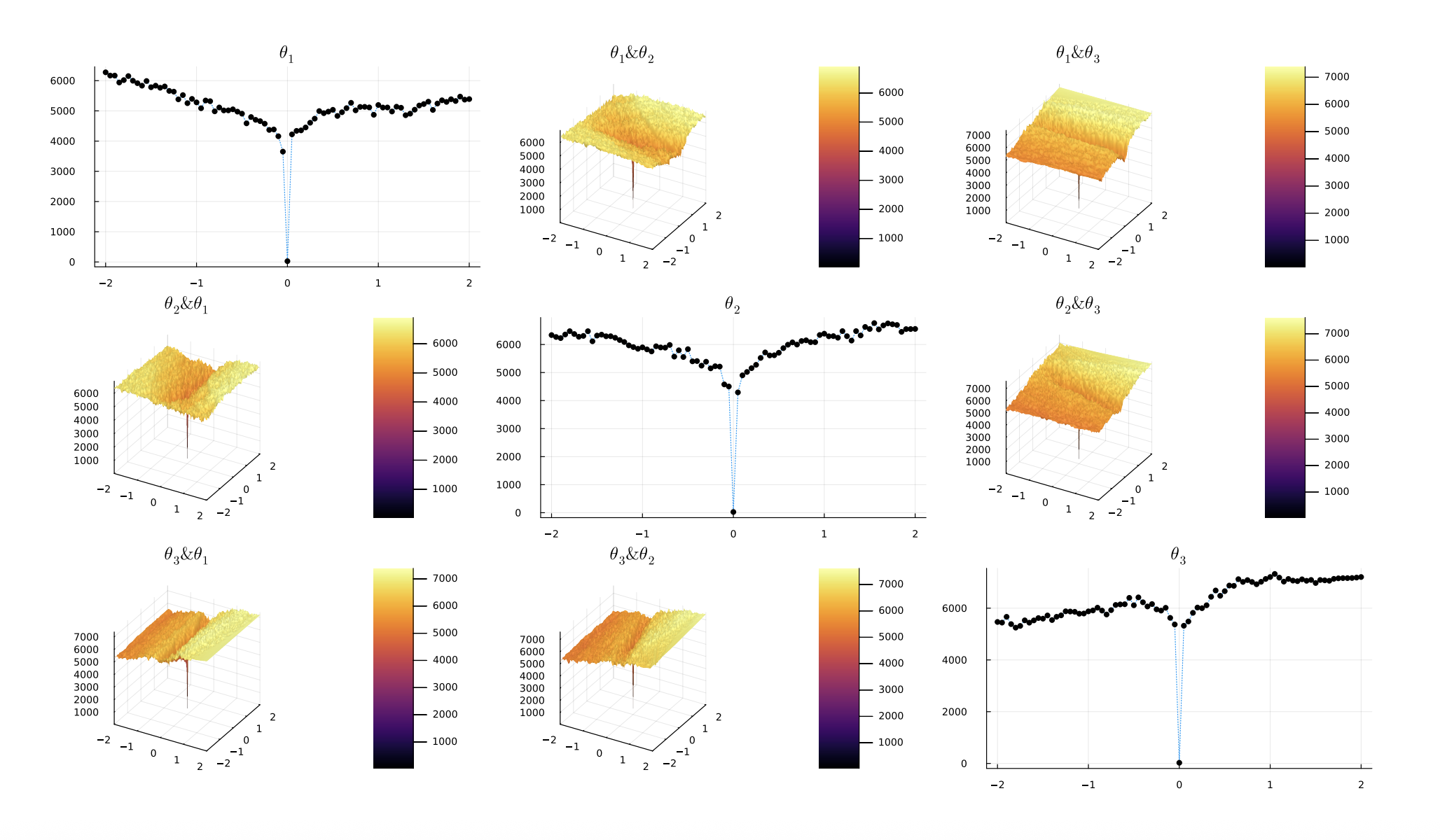
In this paper, we formalize the performance-learnability trade-off in autoregressive forecasting. Our key insight is that the geometry of the loss landscape — the mathematical surface that optimization algorithms navigate during training — changes dramatically with the forecasting horizon. For chaotic systems like weather, this landscape becomes exponentially rougher as we look further into the future. For periodic systems, the roughness grows linearly.
Key Findings
The Loss Landscape Gets Rougher with Longer Horizons
We prove that for chaotic systems, the number of local minima and maxima in the loss landscape grows
exponentially with the training horizon (characterized by the Lyapunov exponent λ). This means that
training a model to predict 10 steps ahead can be exponentially harder than training it to predict just
1 step ahead. As the horizon approaches infinity, the loss landscape actually becomes fractal—making
gradient descent essentially impossible.
Long-Horizon Models Generalize Better
Despite being harder to train, models trained on longer horizons generalize remarkably well to
short-term predictions. We show that a model trained to predict 10 steps ahead will typically perform
better at 1-step predictions than a model trained specifically for 1-step forecasting. This creates our
central trade-off: better performance requires navigating a more difficult optimization landscape.
Optimal Horizons Depend on System Dynamics
Through extensive experiments on systems ranging from the Lorenz attractor to ecological models, we
found that the optimal training horizon is neither one step nor the testing horizon. Instead, it depends
on the underlying dynamics of the system—particularly whether it's chaotic (exponential error growth) or
periodic (linear error growth).
Practical Implications
Our findings challenge common practices in time series forecasting:
Single-step training is rarely optimal: Many practitioners train models to predict just one step ahead, but our theory and experiments show this leaves performance on the table.
Matching training and testing horizons isn't ideal: If you need 5-day weather forecasts, training on exactly 5 days isn't optimal—the best horizon depends on the system's chaos characteristics.
Computational budget matters: With limited training time, shorter horizons might be necessary despite their theoretical disadvantages.
We validated our theory on real-world climate datasets including NOAA sea surface temperatures and ClimSim data, finding that optimal training horizons consistently differed from both single-step and testing horizons.
Beyond Neural Networks
Interestingly, our theory extends beyond neural networks to mechanistic models based on differential equations. When model parameters are unknown, the same trade-offs apply: longer horizons reveal more about system dynamics but create harder optimization problems. This suggests our framework could guide parameter estimation in scientific modeling across fields from climate science to epidemiology.
This work opens new directions for research in time series forecasting, suggesting that understanding the dynamical properties of your system — particularly its chaotic or periodic nature — should guide fundamental training decisions. As we develop larger foundation models for time series, these insights become even more critical for efficient training and deployment.